Dạng toán thường gặp tuyển sinh 10 - Chuyên đề 7. Số học | Toán 10 - Chân trời sáng tạo
Dạng toán thường gặp tuyển sinh 10 - Chuyên đề 7. Số học
Dưới đây là công thức Dạng toán thường gặp tuyển sinh 10 - Chuyên đề 7. Số học
Câu 1: (ts Lào Cai 2022-2023) Chọn ngẫu nhiên một số trong các số tự nhiên từ 1 đến 10. Tính xác suất để số được chọn là số chia hết cho 5.
Lời giải
Không gian mẫu của phép thử là 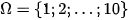
Suy ra 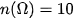
Gọi A là biến cố “Số được chọn chia hết cho 5”
Ta có: 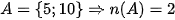
Vậy xác suất của biến cố A là 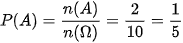
Câu 2: (ts TP HCM 2022-2023) Đại hội Thể thao Đông Nam Á – SEA Games (South East Asian Games) là sự kiện thể thao được tổ chức 2 năm 1 lần với sự tham gia của các vận động viên trong khu vực Đông Nam Á. Việt Nam là chủ nhà của SEA Games 31 diễn ra từ ngày 12 / 5 / 2022 đến ngày 23 / 5 / 2022 . Ở môn bóng đá nam, một bảng đấu gồm có 5 đội A, B, C, D, E thi đấu theo thể thức vòng tròn một lượt (mỗi đội thi đấu đúng một trận với các đội còn lại). Trong mỗi trận đấu, đội thắng được 3 điểm, đội hòa được 1 điểm và đội thua được 0 điểm.
a) Hỏi có tất cả bao nhiêu trận đấu đã diễn ra ở bảng đấu trên?
 trận đấu.
trận đấu.b) Tổng số điểm của các đội là
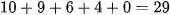 điểm.
điểm.Gọi x là số trận thắng – thua và y là số trận hòa.
Vì có 10 trận nên ta có:
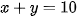 (1)
(1)phương trình: 3x+2y =29
Từ (1) và (2) ta có: x=9 và y=1 .
Mỗi đội có 4 trận đấu với các đội còn lại mà đội A có 10 điểm tức đội A thắng 3 trận hòa 1 trận. Đội B có 9 điểm tức thắng 3 trận thua 1 trận. Đội C có 6 điểm tức thắng 2 trận thua 2 trận. Đội D có 4 điểm tức thắng 1 trận hòa 1 trận. Đội E không có điểm tức thua hết 4 trận.
Vậy trận hòa là của đội A và đội D.
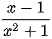 là số nguyên.
là số nguyên.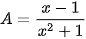

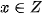 nên
nên 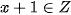 . Khi đó nếu
. Khi đó nếu 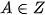 thì
thì 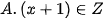
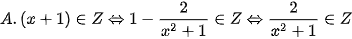

 nên
nên 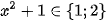
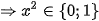
 (tm
(tm  )
) (tm
(tm  )
)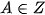
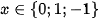 thỏa mãn đề ra
thỏa mãn đề ra