Dạng toán thường gặp tuyển sinh 10 - Chuyên đề 6. Bất đẳng thức. | Toán 9 - Chân trời sáng tạo
Dạng toán thường gặp tuyển sinh 10 - Chuyên đề 6. Bất đẳng thức.
Dưới đây là công thức Dạng toán thường gặp tuyển sinh 10 - Chuyên đề 6. Bất đẳng thức.
Câu 1: (ts Quảng Bình 2022-2023) Cho x, y>0 và thỏa mãn x+y+3xy=5 . Tìm giá trị nhỏ nhất của biểu thức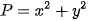 
.
Lời giải
Theo bất đẳng thức Côsi, với x, y>0 ta có: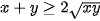 
. ( Dấu "=" xảy ra 
)
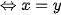Suy ra: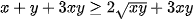 
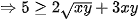( vì theo đề bài: x+y+3xy =5)
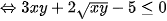
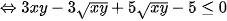
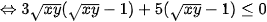
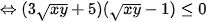
( vì x, y > 0 nên 
)
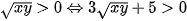Ta có:
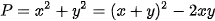
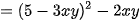(vì x+y+3xy=5 nên x+y=5-3xy)
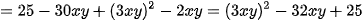
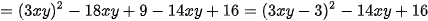
Vì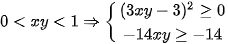 
Suy ra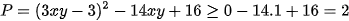 
Dấu "=" xảy ra khi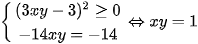 
(thỏa mãn 
)
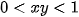Kết hợp các điều kiện: x, y>0; x+y+3xy=5; x=y và ta có x=y=1
vậy GTNN của P = 2 khi x=y=1.
Câu 2: (ts HÀ NỘI 2022-2023) Với các số thực không âm x và y thỏa mãn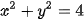 
. Tìm giá trị nhỏ nhất của biểu thức P=x+2y.
Lời giải
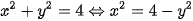
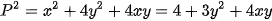
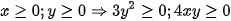nên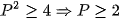 
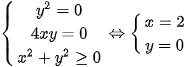
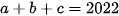
Tìm giá trị nhỏ nhất của biểu thức
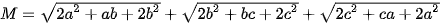
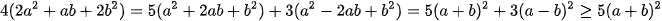
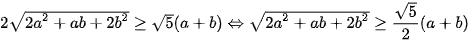(1)
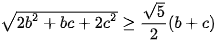(2). Dấu bằng xảy ra khi b=c
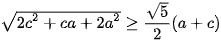(3). Dấu bằng xảy ra khi c=a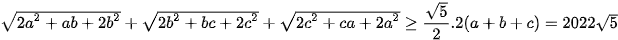
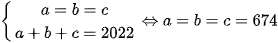
Vậy GTNN của M là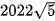 
khi a=b=c=674
Câu 4: (ts BẮC NINH 2022-2023)
a) Chứng minh rằng nếu tất cả các cạnh của một tam giác luôn nhỏ hơn 2 thì diện tích của tam giác đó nhỏ hơn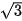 
.
b) Cho các số thực a, b, c sao cho phương trình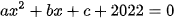 
nhận x=1 là nghiệm.
Tìm giá trị nhỏ nhất của biểu thức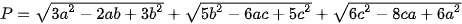 
.
Lời giải
a)
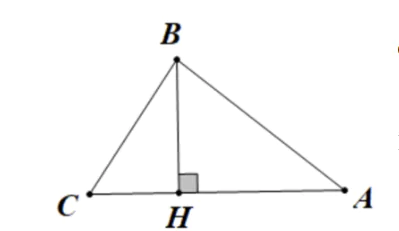
Giả sử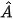 
là góc nhỏ nhất của tam giác ABC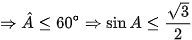 
Kẻ đường cao AH
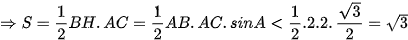(đpcm)
b) Phương trình 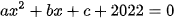nhậ x=1 là nghiệm, ta có 
Ta có: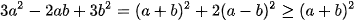 
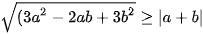
Tương tự ta có:
; 
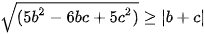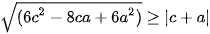
Cộng vế với vế của ba bất đẳng thức trên ta được:
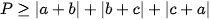
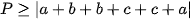
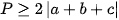
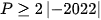
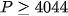
GTNN P=4044 tại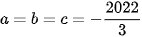 
.
Câu 5: (ts Bắc Giang 2022-2023) Cho các số a, b thỏa mãn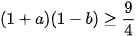 
. Tìm giá trị nhỏ nhất của biểu thức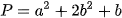 
Lời giải
Với mọi số thực x, y ta có BĐT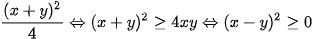 
Áp dụng BĐT trên ta có: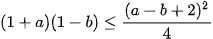 
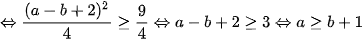
Thay vào P ta được: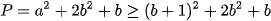 
Ta có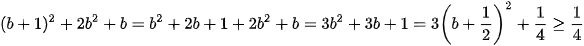 
Từ đó suy ra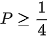 
Dấu "=" xảy ra khi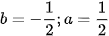 
. Vậy giá trị nhỏ nhất của P là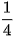 
Câu 6: (ts Hà Nam 2022-2023) Cho hai số a, b thỏa mãn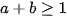 
và a>0 . Tìm giá trị nhỏ nhất của biểu thức: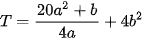 
Lời giải
Ta có: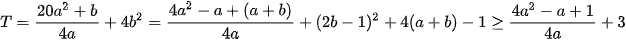 
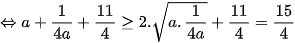
Vậy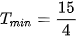 
. Dấu bằng xảy ra khi 
.
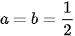Câu 7: (ts Ninh Bình 2022-2023) Biết a, b, c là ba số thực dương thỏa mãn điều kiện a+b+c=1 .
Chứng minh rằng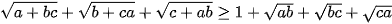 
Lời giải
Áp dụng bất đẳng thức AM-GM ta có
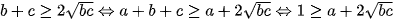
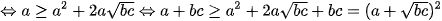
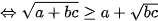(*)Chứng minh tương tự:
(**)
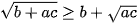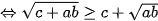(***)Lấy vế cộng vế của (*);(**);(***) ta có:
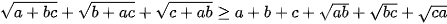(điều phải chứng minh)
.
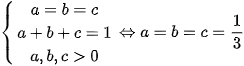