Dạng toán thường gặp tuyển sinh 10 - Chuyên đề 5. Giải bài toán bằng cách lập phương trình – hệ phương trình. | Toán 9 - Chân trời sáng tạo
Dạng toán thường gặp tuyển sinh 10 - Chuyên đề 5. Giải bài toán bằng cách lập phương trình – hệ phương trình.
Dưới đây là công thức Dạng toán thường gặp tuyển sinh 10 - Chuyên đề 5. Giải bài toán bằng cách lập phương trình – hệ phương trình.
Câu 1: (ts Hải Phòng 2022-2023) Bác An thuê nhà với giá 1500000 đồng/tháng, bác phải trả tiền địch vụ giới thiệu là 500000 đồng (tiền dịch vụ chi trả một lần). Gọi x (tháng) là thời gian mà bác An thuê nhà, y (đồng) là tổng số tiền bác phải trả bao gồm tiền thuê nhà trong x (tháng) và tiền dịch vụ giới thiệu.
a) Lập công thức tính y theo x .
b) Tính tổng số tiền bác An phải trả sau khi thuê nhà 5 tháng.
Lời giải
a) Tổng số tiền thuê trong x (tháng) bác An phải trả là 1500000x (đồng).
Tổng số tiền bác phải trả bao gồm tiền thuê nhà trong x (tháng) và tiền dịch vụ giới thiệu là: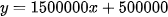
(đồng).
Vậy công thức tính y theo x là: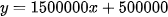
b)
Tổng số tiền bác An phải trả sau khi thuê nhà 5 tháng là: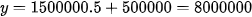 
( đồng).
Câu 2: (ts TP HCM 2022-2023) Giá bán một cái bánh cùng loại ở hai cửa hàng A và B đều là 15 000 đồng, nhưng mỗicửa hàngáp dụng hình thức khuyến mãi khác nhau. Cửa hàng A: đối với 3 cái bánh đầu tiên, giá mỗi cái là 15 000 đồng và từ cái bánh thứ tư trở đi khách hàng chỉ phải trả 75% giá bán. Cửa hàng B: cứ mua 3 cái bánh thì được tặng thêm 1 cái bánh cùng loại.
Bạn Hằng cần đúng 13 cái bánh để tổ chức sinh nhật thì bạn ấy nên mua bánh ở cửa hàng nào để tiết kiệm và tiết kiệm được bao nhiêu tiền so với cửa hàng kia?
Lời giải
Giá bán 1 cái bánh từ thứ tư trở đi ở cửa hàng A là: 75%.15 000 =11 250(đồng)
Số tiền bạn Hằng phải trả khi mua 13 cái bánh ở cửa hàng A là: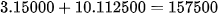 
(đồng).
Để mua được 13 cái bánh ở cửa hàng B, bạn Hằng phải mua 10 cái bánh và được khuyến mãi 3 cái.
Số tiền bạn Hằng phải trả khi mua 10 cái bánh ở cửa hàng B là: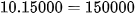 
(đồng).
Do 150 000< 157 500 nên bạn Hằng mua ở cửa hàng B sẽ tiết kiệm hơn, và số tiền tiết kiệm so với khi mua ở cửa hàng A là 157 500 - 150 000 = 7 500 (đồng)
Câu 3: (ts HÀ NỘI 2022-2023) Giải bài toán sau bằng cách lập phuơng trình hoặc hệ phương trình:
Một ô tô và một xe máy cùng khởi hành từ địa điểm A và đi đến địa điểm B. Do vận tốc của ô tô lớn hơn vận tốc của xe máy là 20 km/h nên ô tô đến B sớm hơn xe máy 30 phút. Biết quãng đường AB dài 60km , tính vận tốc của mỗi xe. (Giả định rằng vận tốc mỗi xe là không đổi trên toàn bộ quãng đường AB).
Lời giải
Đổi 30 phút = 0.5 giờ
Gọi vận tốc của xe máy là x (km/h). (ĐK: x>0).
Vận tốc của ô tô là x+20 (km/h)
Thời gian xe máy đi hết quãng đường AB là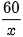 
(giờ)
Thời gian ô tô đi hết quãng đường AB là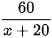 
(giờ)
Vì ô tô đến B sớm hơn xe máy 30 phút = 0.5 giờ nên ta có phương trình:
Ta có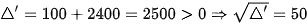 
Phương trình có hai nghiệm phân biệt là: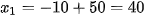
(thỏa mãn).
(không thỏa mãn)
Vậy vận tốc của xe máy là40 (km/h) ; vận tốc của ô tô là 60 (km/h)
Câu 4: (ts Quảng Trị 2022-2023) Nhằm phục vụ khán giả cổ vũ giải bóng đá U23 châu Á, một xưởng may phải may 2000 áo cổ động viên trong một số ngày quy định. Trong ba ngày đầu, mỗi ngày xưởng may đúng số áo theo kế hoạch. Từ ngày thứ tư, nhờ cải tiến kỹ thuật, mỗi ngày xưởng may được nhiều hơn 30 áo so với số áo phải may trong một ngày theo kế hoạch. Vì thế, trước khi hết thời hạn một ngày, xưởng đã may được 1980 áo. Hỏi theo kế hoạch, mỗi ngày xưởng phải may bao nhiêu áo?
Lời giải
Gọi số áo mà xưởng phải may mỗi ngày theo kế hoạch là x (chiếc), 
Thì số ngày phải may theo kế hoạch là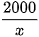 
(ngày).
Số áo may được trong ba ngày đầu là: 3x (chiếc)
Thực tế từ ngày thứ tư, mỗi ngày xưởng may được +30 (chiếc)
Số ngày may thực tế là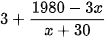 
(ngày).
Vì số ngày may thực tế sớm hơn kế hoạch một ngày nên ta có phương trình: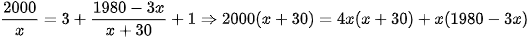 
Giải phương trình ta được: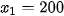 
(thỏa mãn); 
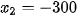(loại);
Vậy theo kế hoạch mỗi ngày xưởng phải may 200 chiếc áo.
Câu 5: (ts Cần Thơ 2022-2023) Anh Thuận đến cửa hàng điện máy mua 1 máy lạnh và một máy giặt để sử dụng trong gia đình. Khi đến mua hàng thì giá tiền của 1 máy lạnh tăng thêm 15% và giá tiền của 1 máy giặt giảm bớt 20% so với giá niêm yết. Vì vậy, anh Thuận thanh toán tổng cộng 19 400 000 đồng khi mua hai món hàng trên. Biết rằng theo giá niêm yết của cửa hàng, tổng giá tiền 2 máy lạnh nhiều hơn tổng giá tiền của 3 máy giặt là 3 000 000 đồng . Hỏi giá tiền niêm yết của 1 máy lạnh và 1 máy giặt là bao nhiêu ?
Lời giải
Gọi giá niêm yết của máy lạnh là x (đồng) (x>0)
Giá niêm yết của máy giặt là y(đồng) (y>0)
Giá tiền của máy lạnh khi tăng thêm15% so với giá niêm yết là :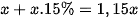
( đồng)
Giá tiền cuar máy giặt khi giảm bớt 20% so với giá niêm yết là :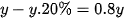 
( đồng)
Anh Thuận thanh toán tổng cộng 19 400 000 đồng khi mua hai món hàng trên nên ta có :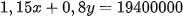
(1)
Tổng giá tiền 2 máy lạnh nhiều hơn tổng giá tiền của 3 máy giặt là 3 000 000 đồng nên ta có :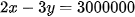
(2)
Từ (1) và (2) ta có hệ phương trình :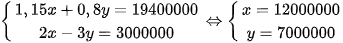
Vậy giá niêm yết của máy lạnh là 12 000 000 (đồng) và của máy giặt là 7 000 000 (đồng).
Câu 6: (ts Bắc Kạn 2022-2023) Bạn A dự định mua 2kg quả xoài và 2kg quả vải hết 100 000 đồng. Thực tế, A mua 3kg quả xoài và 1kg quả vải hết 90 000 đồng. Tính giá của 1kg quả xoài và giá của 1kg quả vải.
Lời giải
Gọi giá tiền của 1kg quả xoài là x (đồng) ( x>0 )
và Giá tiền của 1kg quả vải là y (đồng) (y>0 )
Bạn A dự định mua 2kg quả xoài và 2kg quả vải hết 100 000 đồng nên ta có phương trình: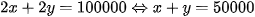
(1)
Bạn A thực tế mua 3kg quả xoài và 1kg quả vải hết 90 000 đồng nên ta có phương trình: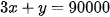
(2)
Từ (1) và (2) ta có hệ phương trình: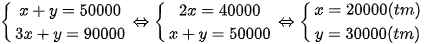 
Vậy giá 1kg quả xoài là 20 000 đồng và giá 1kg quả vải là 30 000 đồng.
Câu 7: (ts Khánh Hòa 2022-2023) Nhằm đáp ứng nhu cầu sử dụng khẩu trang chống dịch COVID-19, theo kế hoạch, 1 tổ sản xuất của một nhà máy dự định làm 720000 khẩu trang. Do áp dụng kĩ thuật mới nên I đã sản xuất vượt kế hoạch 15% và tổ II vượt kế hoạch 12% , vì vậy họ đã làm được 819000 khẩu trang. Hỏi theo kế hoạch số khẩu trang của mỗi tổ sản xuất là bao nhiêu?
Gọi y là số khẩu trang tổ II sản xuất theo kế hoạch.
(Điều kiện:
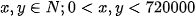)Theo dự định:
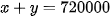
Theo thực tế:
Số khẩu trang tổ II làm được: 112%.y hay 1,12.y (khẩu trang)
Ta có phương trình
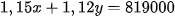
Ta được hệ phương trình:
Giải tìm được
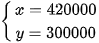(Nhận)Vậy theo kế hoạch tổ I sản xuất 420000 khẩu trang, tổ II sản xuất 300000 khẩu trang.
Gọi x, y (giờ) lần lượt là thời gian hoàn thành công việc của hai đội khi làm riêng, x>0, y>0.
Suy ra trong một giờ đội thứ nhất hoàn thành được
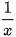công việc, đội thứ hai hoàn thành được 
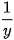công việc.
