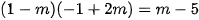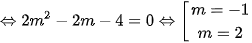Dạng toán thường gặp tuyển sinh 10 - Chuyên đề 3- Phương trình. | Toán 9 - Kết nối tri thức
Dạng toán thường gặp tuyển sinh 10 - Chuyên đề 3- Phương trình.
Dưới đây là công thức Dạng toán thường gặp tuyển sinh 10 - Chuyên đề 3- Phương trình.
Câu 1: (ts Nghệ An 2022-2023) Giải phương trình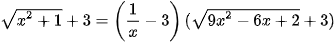 
(1)
Lời giải
ĐKXĐ: x≠0
Ta có: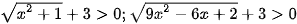 
nên để (1) có nghiệm thì 
.
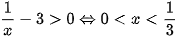Do đó điều kiện để (1) có nghiệm là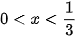 
(1) 
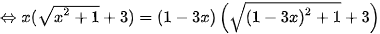
Đặt a=x, b=1-3x (a, b >0) khi đó ta có phương trình:
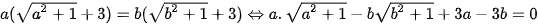
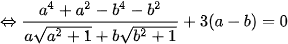
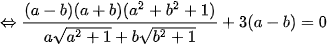
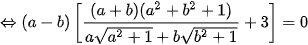
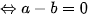(do a, b > 0 nên 
)
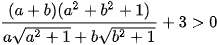Do đó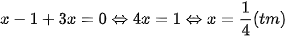 
Vậy phương trình có nghiệm 
.
Câu 2: (ts Bà Rịa Vũng Tàu 2022-2023) Giải phương trình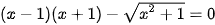 
Lời giải
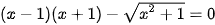
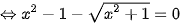
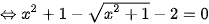(1)
Đặt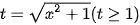 
, phương trình (1) trở thành:
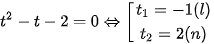
Với 
Vậy phương trình có 
.
Câu 3: (ts Điện Biên 2022-2023) Cho phương trình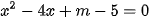 
(m là tham số). Tìm giá trị của m để phương trình có hai nghiệm phân biệt 
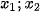thoả mãn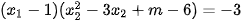 
Lời giải
Ta có: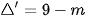
Phương trình có hai nghiệm phân biệt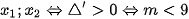 
Theo hệ thức Vi-et ta có: 
Vì 
là nghiệm của phương trình nên :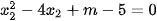
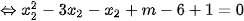
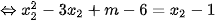
Mà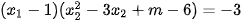 
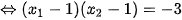
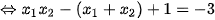
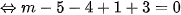
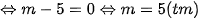
Vậy với m = 5 thì phương trình có hai nghiệm phân biệt 
thỏa mãn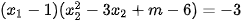 
Câu 4. (ts Sơn La 2022-2023)Giải phương trình: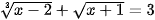 
Lời giải
ĐKXĐ: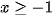 
Đặt 
(1)
Ta có 
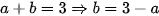(2)
Từ (1), (2) suy ra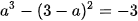 
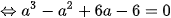
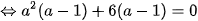
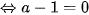( do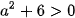 
)
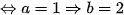
Ta có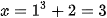 
(thỏa mãn)
Vậy phương trình có nghiệm là x=3.
; 
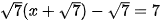
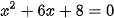
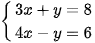
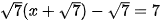
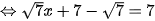
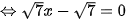
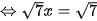
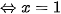
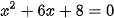
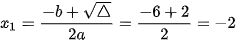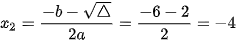
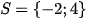
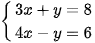
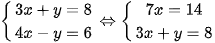
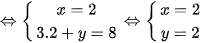
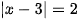
b)
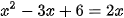
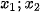
Lời giải
a)
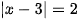
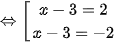
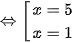
Vậy phương trình có tập nghiệm
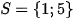
b)
.
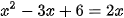
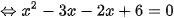
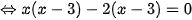
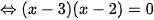
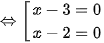
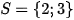có hai nghiệm là 
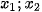. Không giải phương trình, hãy tính giá trị của biểu thức: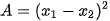 
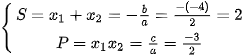
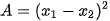
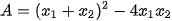
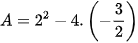
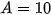
(1) (với m là tham số).a) Chứng minh rằng với mọi giá trị của m phương trình (1) luôn có hai nghiệm phân biệt.
b) Gọi
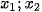là hai nghiệm của phương trình (1) . Tìm tất cả giá trị của m để 
.
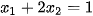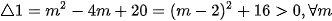
Do đó phương trình (1) có hai nghiệm phân biệt với mọi m.
b) Theo câu a) ta có với mọi giá trị của m phương trình đã cho có hai nghiệm phân biệt
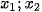
Nên ta có
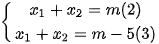
Theo giả thiết ta có
Từ (2) và (4) ta có
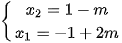
Thay
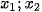vào (3) ta được 
