Dạng toán thường gặp tuyển sinh 10 - Chuyên đề 1. Căn bậc hai | Toán 9 - Kết nối tri thức
Dạng toán thường gặp tuyển sinh 10 - Chuyên đề 1. Căn bậc hai
Dưới đây là công thức Dạng toán thường gặp tuyển sinh 10 - Chuyên đề 1. Căn bậc hai
Câu 1: (TS Quảng Ninh 2022-2023)
a) Thực hiện phép tính: 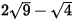
b) Rút gọn biểu thức: 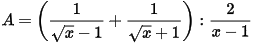 với
với 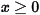 và
và 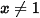
Lời giải
a) Ta có 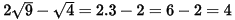
b) 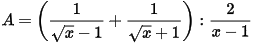 với
với 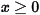 và
và 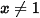
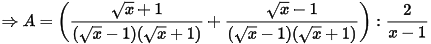
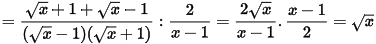
Câu 2: (TS Lạng Sơn 2022-2023)
a) Tính giá trị các biểu thức: 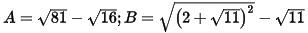 .
.
b) Cho biểu thức: 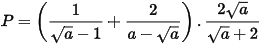 với a > 0 và a ≠ 1.
với a > 0 và a ≠ 1.
1. Rút gọn biểu thức P.
2. Tính giá trị của P khi a = 3 + 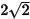
Lời giải
a) Tính giá trị các biểu thức:
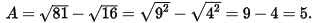
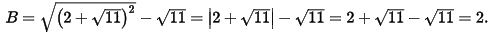
b) Xét biểu thức 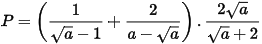 với a > 0 và a ≠ 1.
với a > 0 và a ≠ 1.
1. Rút gọn biểu thức P:
Với a > 0 và a ≠ 1, ta có: 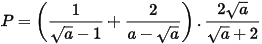
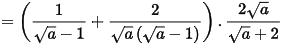
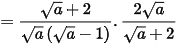
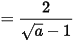 .
.
2. Tính giá trị của P khi a = 3 + 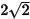 :
:
Khi a = 3 + 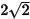 (thoả mãn điều kiện xác định), ta có:
(thoả mãn điều kiện xác định), ta có:
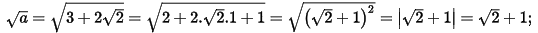
Suy ra: 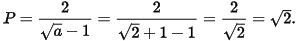
Vậy 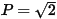 khi a = 3 +
khi a = 3 + 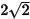 .
.
Câu 3: (TS Thái Bình 2022 - 2023) Cho biểu thức: 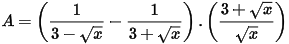 với x > 0 và x ≠ 9.
với x > 0 và x ≠ 9.
1. Rút gọn biểu thức A.
2. Tính giá trị của biểu thức A khi x = 4.
3. Tìm tất cả các giá trị nguyên của x để 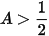 .
.
Lời giải
1. Rút gọn biểu thức A.
Ta có 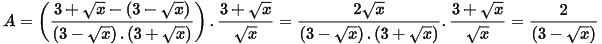
Vậy với x > 0 và x ≠ 9 thì 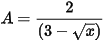
2. Tính giá trị của biểu thức A khi x = 4.
Với x = 4 thoả mãn điều kiện xác định, thay vào ta có 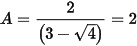
Vậy với x = 4 thì A = 2
3. Tìm tất cả các giá trị nguyên của x để 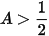 .
.
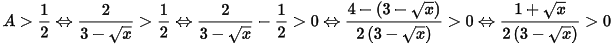
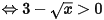 (do
(do 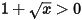 )
) 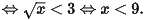
Do 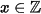 và kết hợp đkxđ
và kết hợp đkxđ 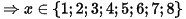
Câu 4: (TS Nam Định 2022 - 2023)
a) Rút gọn biểu thức 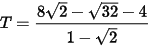 .
.
b) Tìm điều kiện xác định và rút gọn biểu thức 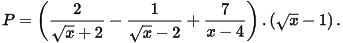
Lời giải
a) 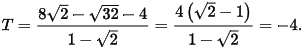
b) Điều kiện x ≥ 0; x ≠ 4.
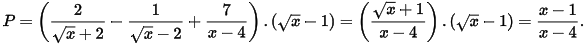
Câu 5: (TS Thanh Hoá 2022 - 2023) Cho biểu thức 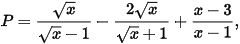 với x ≥ 0, x ≠ 1.
với x ≥ 0, x ≠ 1.
1. Rút gọn biểu thức P.
2. Tìm các giá trị của x để 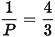 .
.
Lời giải
1. Với x ≥ 0, x ≠ 1, ta có:
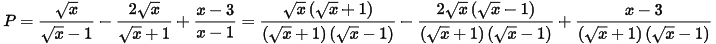
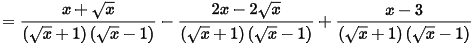
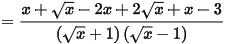
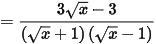
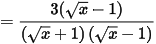
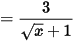 .
.
Vậy 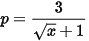 (Với x ≥ 0, x ≠ 1).
(Với x ≥ 0, x ≠ 1).
Câu 6: (TS Hà Nội 2022 - 2023) Cho hai biểu thức 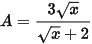 và
và 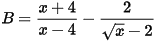 với x ≥ 0, x ≠ 4.
với x ≥ 0, x ≠ 4.
1) Tính giá trị của biểu thức A khi x = 9.
2) Chứng minh 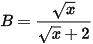 .
.
3) Tìm số nguyên dương x lớn nhất thoả mãn 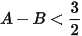 .
.
Lời giải
1) Thay x = 9 vào biểu thức A ta được 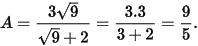
Vậy với x = 9 ta được 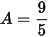 .
.
2) Với x ≥ 0; x ≠ 4 ta có:
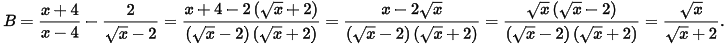
Vậy 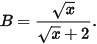
3) Ta có:
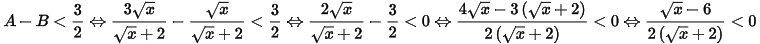
Mà 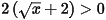 do đó
do đó 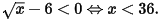
Kết hợp x ≥ 0; x ≠ 4, mà x là số nguyên lớn nhất nên x = 35.
Vậy x = 35 là giá trị cần tìm.
Câu 7: (TS Bình Dương 2022 - 2023) Thực hiện phép tính: 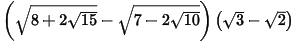
Lời giải
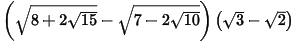
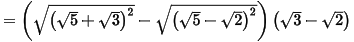
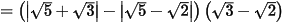
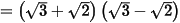
= 3 - 2 = 1
Câu 8: (TS Bình Định 2022 - 2023) Cho biểu thức 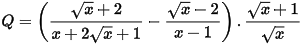 ; x > 0; x ≠ 1.
; x > 0; x ≠ 1.
a) Rút gọn biểu thức Q.
b) Tìm số nguyên x để Q có giá trị nguyên lớn nhất.
Lời giải
a) 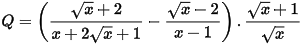
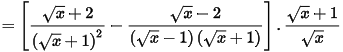
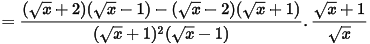
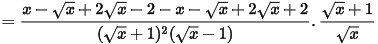
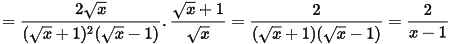
b) Q nguyên 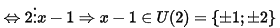

Vậy x = 2 thì Q đạt giá trị nguyên lớn nhất.