CÁC QUY TẮC TÍNH XÁC SUẤT : Nếu biết xác suất xảy ra của biến cố A, xác suất xảy ra của biến cố B, làm thế nào để tính xác suất xảy ra biến cố A hoặc biến cố B, xác suất xảy ra biến cố A và biến cố B? Bài học này đưa ra các quy tắc tính xác suất nhằm mục đích giúp ta trả lời các câu hỏi trên.

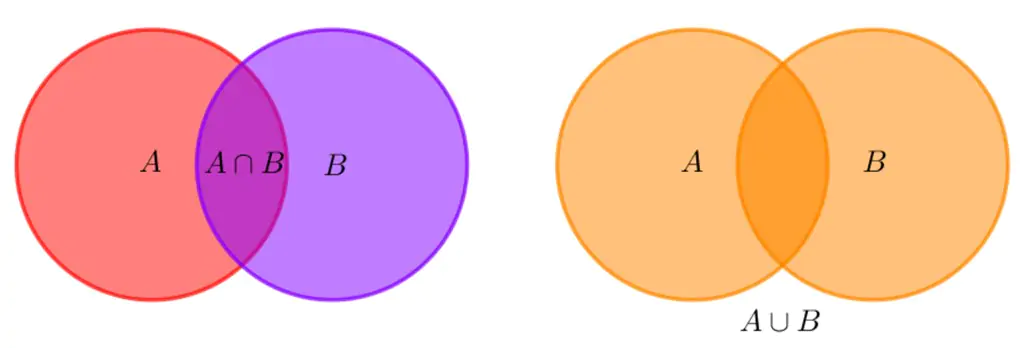
1. Biến cố hợp

Cho $A$ và B là hai biến cố. Biến cố: " $A$ hoặc $B$ xảy ra" được gọi là biến cố hợp của $A$ và $B$ và được kí hiệu là .

Giả sử A,B là tập con của không gian mẫu 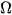. Biến cố hợp của A và B là tập con của không gian mẫu .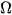

Nhận xét: Ta có thể hiểu biến cố hợp của A và B là biến cố mà ít nhất một trong hai biến $A$ và $B$ xảy ra.

Tổng quát: Cho k biến cố 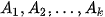. Biến cố: “ít nhất một trong các biến cố 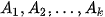xảy ra” được gọi là biến cố hợp của k biến cố 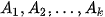và được kí hiệu là .

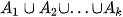2. Biến cố giao

Cho $A$ và $B$ là hai biến cố. Biến cố: " Cả $A$ và $B$ đều xảy ra" được gọi là biến cố giao của A và $B$ được kí hiệu là AB hay .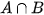

Giả sử A,B là tập con của không gian mẫu 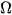$.$ Biến cố giaoAB là tập con 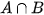của không gian mẫu .

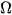Tổng quát: Cho $k$ biến c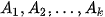ố . Biến cố: “ 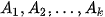đều xảy ra” được gọi là biến cố giao của k biến cố 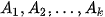và được kí hiệu là  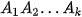hay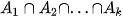

3. Biến cố độc lập

Hai biến cố A và $B$ được gọi là độc lập nếu việc xảy ra hay không xảy ra của biến cố này không ảnh hưởng tới xác suất xảy ra của biến cố kia. Nếu cặp biến cố (A,B) độc lập thì các cặp biến cố 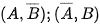và 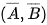cũng độc lập.

Ví dụ: Có hai lọ hoa. Lọ I cắm 5 bông hoa hồng và 3 bông hoa cúc. Lọ II cắm 4 bông hoa hồng và 5 bông hoa thược dược. Lấy ngẫu nhiên đồng thời từ mỗi lọ một bông hoa. Xét hai biến cố sau: $A:$ "Lấy được bông hoa hồng từ lọ I", $B:$ "Lấy bông hoa hồng từ lọ II". Chứng tỏ rằng $A$ và $B$ độc lập.

Giải. Dù $A$ có xảy ra (lấy được bông hoa hồng) hay $A$ không xảy ra (lấy được bông hoa cúc) ta đều có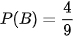

Dù $B$ có xảy ra (lấy được được bông hoa hồng) hay $B$ không xảy ra (lấy được bông hoa thược dược) ta đều có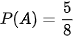

Việc xảy ra hay không xảy ra của biến cố này không ảnh hưởng tới xác suất xảy ra của biến cố kia. Vậy $A$ và $B$ độc lập.

4. Biến cố xung khắc

Biến cố $A$ và biến cố $B$ được gọi là xung khắc nếu $A$ và $B$ không đồng thời xảy ra.

Hai biến cố $A$ và $B$ xung khắc khi và chỉ khi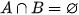

Biến cố $A$ và biến cố đối 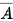(biến cố không xảy ra $A$) là hai biến cố xung khắc.

Ví dụ : Gieo đồng thời hai con xúc xắc cân đối, đồng chất. Xét các biến cố sau:

$\mathrm{A:}$ "Tổng số chấm xuất hiện trên hai con xúc xắc lớn hơn hoặc bằng 7 ";

$B:$ "Tổng số chấm xuất hiện trên hai con xúc xắc nhỏ hơn hoặc bằng 4 ";

$\mathrm{C:}$ "Tổng số chấm xuất hiện trên hai con xúc xắc là số nguyên tố".

Trong các cặp biến cố $A$ và $\mathrm{B;}$ $A$ và C; $B$ và C, cặp biến cố nào xung khắc? Tại sao?

Giải. Cặp biến cố $A$ và $B$ là xung khắc vì $A$ và $B$ không đồng thời xảy ra.

Cặp biến cố $A$ và $C$ không xung khắc vì nếu tổng số chấm xuất hiện trên hai con xúc xắc bằng 7 thì cả $A$ và $C$ xảy ra.

Cặp biến cố $B$ và $C$ không xung khắc vì nếu tổng số chấm xuất hiện trên hai con xúc xắc bằng 3 thì cả $B$ và $C$ xảy ra.