Bài tập thực tế Toán 10. Mệnh đề tập hợp | Toán 10 - Cánh diều
Bài tập thực tế Toán 10. Mệnh đề tập hợp
Dưới đây là công thức Bài tập thực tế Toán 10. Mệnh đề tập hợp
Câu 1: Cho hai tập hợp 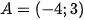 và
và 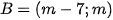 . Tìm m để
. Tìm m để 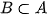
A.  B.
B.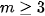 C. m=3 D. m>3
C. m=3 D. m>3
Chọn C
Điều kiện:  .
.
Để 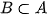 khi và chỉ khi
khi và chỉ khi 
Câu 2: Cho m là một tham số thực và hai tập hợp  . Tất cả các giá trị m để
. Tất cả các giá trị m để  là
là
A. 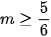 B.
B.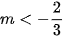 C.
C. 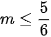 D.
D. 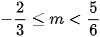
Chọn D
Ta có 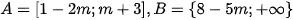
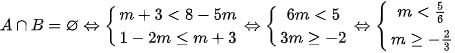
Câu 3: Cho hai tập hợp 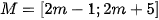 và
và 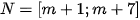 . Tổng tất cả các giá trị của m để hợp của hai tập hợp M và N là một đoạn có độ dài bằng 10 là
. Tổng tất cả các giá trị của m để hợp của hai tập hợp M và N là một đoạn có độ dài bằng 10 là
A. 4 B.-2 C. 6 D.10
Chọn A
Nhận thấy M, N là hai đoạn cùng có độ dài bằng 6, nên để 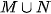 là một đoạn có độ dài bằng 10 thì ta có các trường hợp sau:
là một đoạn có độ dài bằng 10 thì ta có các trường hợp sau:
* 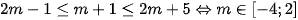 (1)
(1)
Khi đó 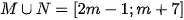 , nên
, nên 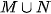 là một đoạn có độ dài bằng 10 khi:
là một đoạn có độ dài bằng 10 khi: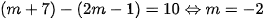 .
.
* 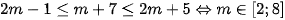
Khi đó 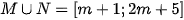 , nên
, nên 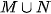 là một đoạn có độ dài bằng 10 khi:
là một đoạn có độ dài bằng 10 khi: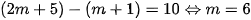
Vậy Tổng tất cả các giá trị của m để hợp của hai tập hợp M và N là một đoạn có độ dài bằng 10 là -2+6 = 4.
Câu 4: Cho hai tập hợp 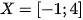 và
và 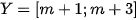 . Tìm tất cả các giá trị
. Tìm tất cả các giá trị 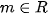 sao cho
sao cho 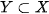 .
.
A. 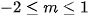 B.
B.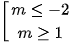 C.
C. 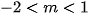 D.
D.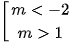
Chọn A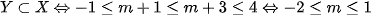 Vậy chọn đáp án A.
Vậy chọn đáp án A.
HS chọn đáp án B và D do đọc không kỹ đề hoặc hiểu sai khái niệm tập hợp con thành 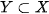
HS chọn đáp án C do hiểu khái niệm tập hợp con thành khái niệm tập hợp con thực sự.
Câu 5: Cho tập hợp 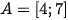 và
và 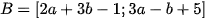 với
với 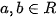 . Khi A=B thì giá trị biểu thức
. Khi A=B thì giá trị biểu thức 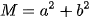 bằng?
bằng?
A. 2 B.5 C. 31 D.25
Ta có
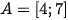 ,
, 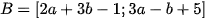 . Khi đó:
. Khi đó: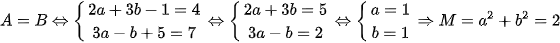
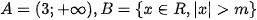 . Có bao nhiêu giá trị nguyên của tham số
. Có bao nhiêu giá trị nguyên của tham số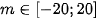 để tập hợp
để tập hợp 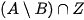 có không quá 10 phần tử?
có không quá 10 phần tử?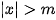 (1)
(1)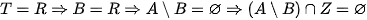
Trường hợp 2:
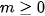
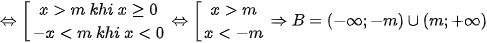
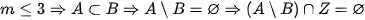
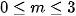 thoả mãn yêu cầu bài toán.
thoả mãn yêu cầu bài toán.
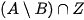 có không quá 10 phần tử khi và chỉ khi tập hợp
có không quá 10 phần tử khi và chỉ khi tập hợp 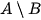 có không quá 10
có không quá 10phần tử là số nguyên
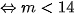 .
.Kết hợp điều kiện suy ra
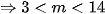 thoả mãn yêu cầu bài toán.
thoả mãn yêu cầu bài toán.Kết hợp trường hợp 1 và 2 suy ra m < 14.
Mặt khác,
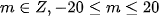 nên có 34 giá trị tham số m thỏa mãn bài toán.
nên có 34 giá trị tham số m thỏa mãn bài toán.