Bài tập thực tế Toán 10. Hệ thức lượng trong tam giác. | Toán 9 - Cánh diều
Bài tập thực tế Toán 10. Hệ thức lượng trong tam giác.
Dưới đây là công thức Bài tập thực tế Toán 10. Hệ thức lượng trong tam giác.
Câu 1: Tính khoảng cách. Một nhân viên kiểm lâm đang đi trên đường nghiêng một góc 5° so với đường thẳng đứng để hướng về tháp quan sát cao 100 feet. Góc độ cao từ chân lên đỉnh tháp là 40° . Tính khoảng cách từ nhân viên kiểm lâm đến chân tháp vào thời điểm đó.
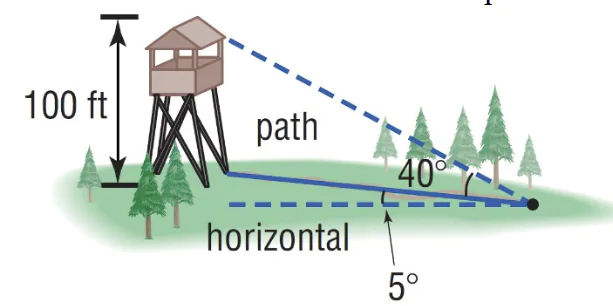
Lời giải
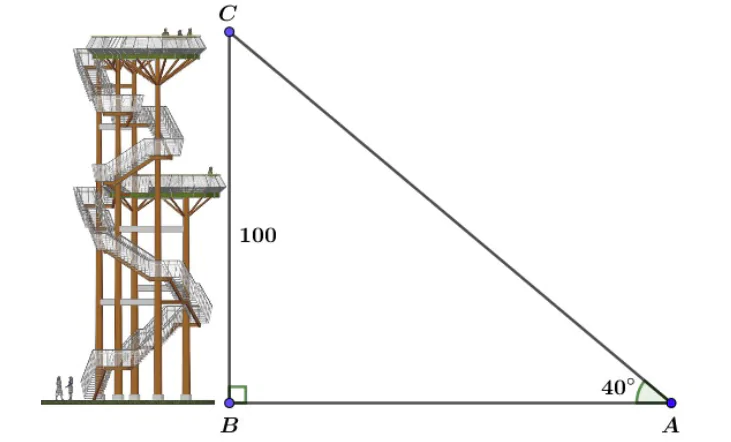
Giả sử nhân viên kiểm lâm tại thời điểm đó đang đứng tại điểm A, ta kí hiệu chân tháp là B và đỉnh tháp là C .
Xét  vuông tại B có
vuông tại B có  và
và 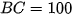 nên
nên 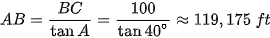
Vậy khoảng cách từ nhân viên đến chân tháp vào thời điểm đó xấp xỉ 119,175 ft.
Câu 2: Tìm chiều cao của một ngọn núi. Để đo được chiều cao của một ngọn núi, một nhân viên trắc địa nhìn đỉnh núi tại hai vị trí cách nhau 900 mét nằm trên một đường thẳng đến ngọn núi (quan sát hình minh họa). Lần quan sát đầu tiên người này nhìn đỉnh núi với một góc nâng là 47° và lần thứ hai nhìn đỉnh núi với một góc nâng là 35° . Giả sử máy toàn đạc cao 2 mét, tìm chiều cao h của ngọn núi.
Lời giải
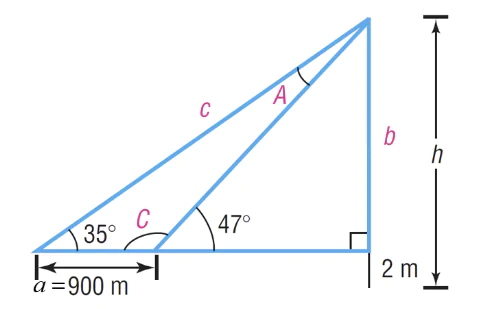 với h là chiều cao của ngọn núi.
với h là chiều cao của ngọn núi.
Ta có: 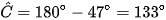
Mặt khác: 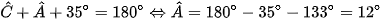
Áp dụng định lí sin ta có: 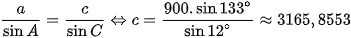 (mét)
(mét)
Mà: 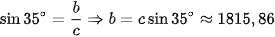 (mét).
(mét).
Vậy chiều cao của ngọn núi là: 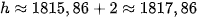 (mét)
(mét)
Câu 3: Thiết kế mái che. Một mái hiên che cửa kính có độ cao 88 inch và tạo với vách tường một góc 50° .Mục đích của mái hiên là che được ánh nắng mặt trời chiếu vào nhà khi góc giữa tia sáng mặt trời với mặt đất lớn hơn 65°. Xem hình vẽ. Tính độ dài L của mái hiên.
Lời giải
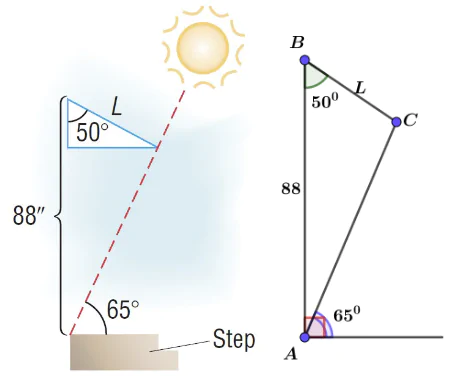
Ta có 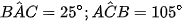
Áp dụng định lý sin vào tam giác ABC ta có: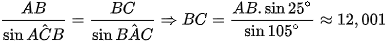
Vậy chiều dài L của mái hiên xấp xỉ 12,001 inch.
Câu 4: Hai chiếc tàu thuỷ cùng xuất phát vị trí A, đi thẳng theo hướng tạo với nhau một góc 60°. Tàu B chạy với vận tốc 50 km/h. Tàu C chạy với vận tốc 20 km/h . Hỏi sau 2 giờ thì hai tàu cách nhau bao nhiêu km?
Lời giải
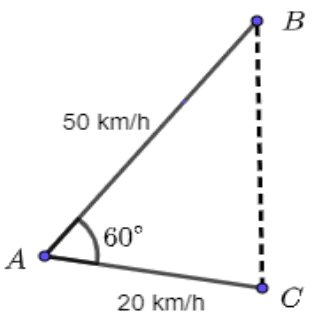
Sau 2h tàu A đi đươc: AB = 2.50 = 100 (km)
Tàu B đi được: AC = 2.20 = 40 (km)
Sau 2h hai tàu cách nhau: 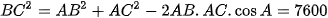 km.
km.
Câu 5: Để đo chiều cao AB của một cái tháp, người ta chọn hai điểm C, D trên mặt đất cách nhau 89m. Từ C,D lần lượt nhìn lên đỉnh B của tháp dưới các góc lần lượt là 30° và 40° (tham khảo hình vẽ).
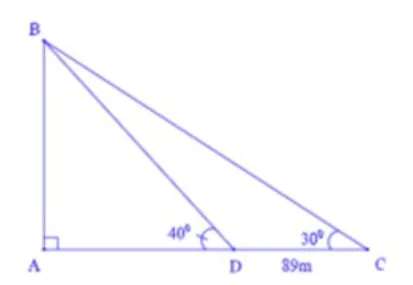
 vuông tại A nên
vuông tại A nên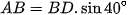
Mà trong tam giác BCD có
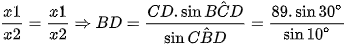
Vậy
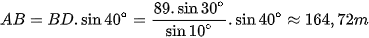
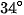 và
và 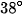 . Tính chiều cao của ngọn núi.
. Tính chiều cao của ngọn núi.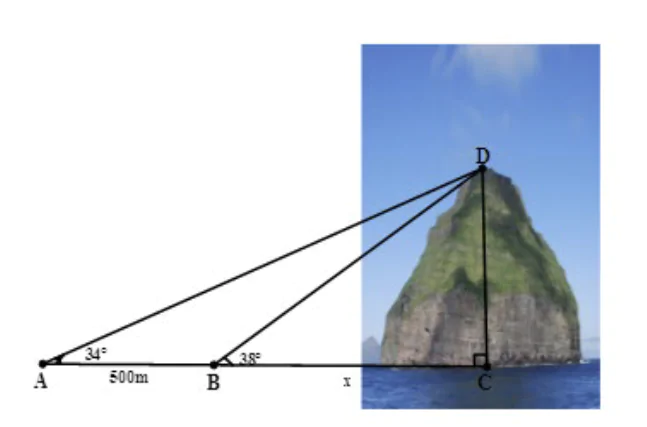
Trong tam giác vuông ACD ta có :
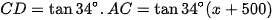
Mặt khác trong tam giác vuông BCD ta có :
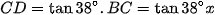
Từ đây suy ra:
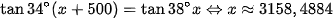
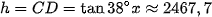 .
.