Bài tập thực tế Toán 10. Bất phương trình và hệ bất phương trình bậc nhất hai ẩn. | Toán 10 - Cánh diều
Bài tập thực tế Toán 10. Bất phương trình và hệ bất phương trình bậc nhất hai ẩn.
Dưới đây là công thức Bài tập thực tế Toán 10. Bất phương trình và hệ bất phương trình bậc nhất hai ẩn.
Câu 1: Một gian hàng trưng bày bàn và ghế rộng 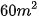 . Diện tích để kê một chiếc ghế là
. Diện tích để kê một chiếc ghế là 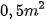 , một chiếc bàn là
, một chiếc bàn là 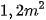 . Gọi x là số chiếc ghế, y là số chiếc bàn được kê. Bất phương trình bậc nhất hai ẩn ,x y cho phần mặt sàn để kê bàn và ghế là bất phương trình nào sau đây? Biết diện tích mặt sàn dành cho lưu thông tối thiểu là
. Gọi x là số chiếc ghế, y là số chiếc bàn được kê. Bất phương trình bậc nhất hai ẩn ,x y cho phần mặt sàn để kê bàn và ghế là bất phương trình nào sau đây? Biết diện tích mặt sàn dành cho lưu thông tối thiểu là  .
.
Lời Giải
Điều kiện: 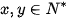
Vì diện tích mặt sàn dành cho lưu thông tối thiểu là  , do đó diện tích phần mặt sàn để kê bàn và ghế tối đa là:
, do đó diện tích phần mặt sàn để kê bàn và ghế tối đa là: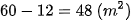
Diện tích để kê một chiếc ghế là 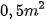 , nên diện tích để kê x chiếc ghế là
, nên diện tích để kê x chiếc ghế là 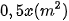
Diện tích để kê một chiếc bàn là 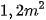 , nên diện tích để kê y chiếc bàn là
, nên diện tích để kê y chiếc bàn là 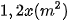
Tổng diện tích cho phần mặt sàn để kê x chiếc ghế và y chiếc bàn là: 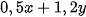
Do đó, bất phương trình cần tìm là: 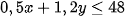
Câu 2: Trong 1 lạng (100 g) thịt bò chứa khoảng 26 g protein, 1 lạng cá rô phi chứa khoảng 20 g protein. Trung bình trong một ngày, một người phụ nữ cần tối thiểu 46 g protein. Gọi ,x y lần lượt là số lạng thịt bò và số lạng cá rô phi mà một người phụ nữ nên ăn trong một ngày. Bất phương trình bậc nhất hai ẩn ,x y để biểu diễn lượng protein cần thiết cho một người phụ nữ trong một ngày là
Lời Giải
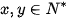
Lượng protein trong x lạng thịt bò là
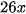 g
gLượng protein trong y lạng cá rô phi là
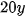 g
gLượng protein trong x lạng thịt bò và y lạng cá rô phi là
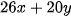
Vì lượng protein tối thiểu là 46g nên ta có bất phương trình:
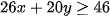
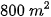 . Nếu trồng đậu trên diện tích
. Nếu trồng đậu trên diện tích 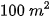 thì cần 20 công làm và thu được 3000000 đồng. Nếu trồng cà thì trên diện tích
thì cần 20 công làm và thu được 3000000 đồng. Nếu trồng cà thì trên diện tích 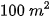 cần 30 công làm và thu được 4000000 đồng. Hỏi cần trồng mỗi loại cây trên diện tích là bao nhiêu để
cần 30 công làm và thu được 4000000 đồng. Hỏi cần trồng mỗi loại cây trên diện tích là bao nhiêu đểthu được nhiều tiền nhất khi tổng số công làm không quá 180 công.
Ta có thu nhập thu được là
 đồng.
đồng.Tổng số công là

Theo giả thiết có
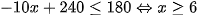
Mà hàm số S(x) là hàm nghịch biến trên R nên S(x) đạt giá trị lớn nhất khi
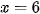
Do đó cần trồng
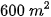 đậu,
đậu,  cà để thu được nhiều tiền nhất khi tổng số công làm không quá 180 công.
cà để thu được nhiều tiền nhất khi tổng số công làm không quá 180 công.được 20 điểm thưởng, mỗi lít nước táo nhận được 80 điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước trái cây mỗi loại để được số tiền thưởng là lớn nhất?
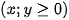
Số điểm thưởng của đội chơi này là
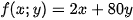
Số gam đường cần dùng là
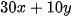 (g).
(g).Số lít nước cần dùng là
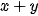 (l).
(l).Số gam hương liệu cần dùng là
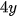 (g).
(g).Vì trong cuộc thi pha chế, mỗi đội chơi sử dụng tối đa 24g hương liệu, 9 lít nước và 210g đường nên ta có hệ bất phương trình sau
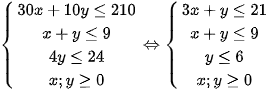
Bài toán trở thành tìm giá trị lớn nhất của hàm sồ(x;y) trên miền nghiệm của hệ bất phương trình (*).
Miền nghiệm của hệ bất phương trình (*) là ngũ giác OABCD
Trong đó

Suy ra f(3;6) là giá trị lớn nhất của hàm số f(x; y) trên miền nghiệm của hệ (*).
Như vậy để được số điểm thưởng lớn nhất cần pha chế 3 lít nước cam và 6 lít nước táo.
Theo giả thuyết, x và y thỏa mãn điều kiện:
 và
và 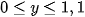
Khi đó chi phí mua x (kg) thịt bò và y (kg) thịt lợn là:
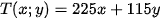 (nghìn đồng).
(nghìn đồng).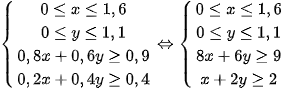 (*)
(*)Trong các nghiệm của hệ bất phương trình (*) , tìm nghiệm
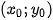 sao cho
sao cho 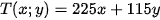 đạt giá trị nhỏ nhất.
đạt giá trị nhỏ nhất.Trong mặt phẳng tọa độ, ta sẽ biểu diễn phần mặt phẳng chứa điểm
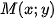 thỏa mãn (*) .
thỏa mãn (*) .Miền nghiệm của hệ (*) là miền bên trong của tứ giác lồi và cả biên (như hình vẽ)
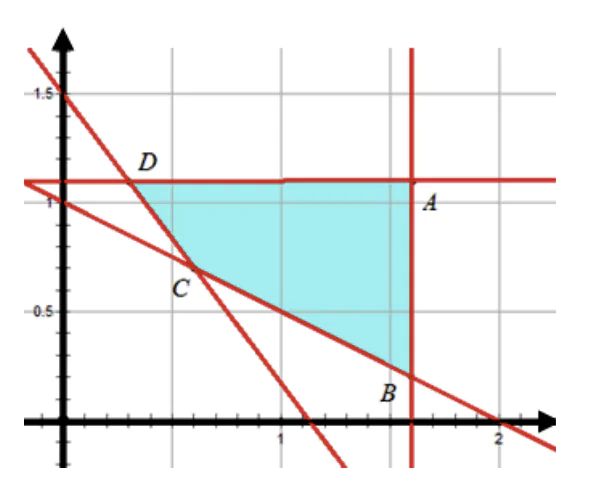
Ta có
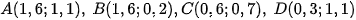
Kiểm tra được x=0,3 và y=1,1 thì
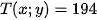 (nghìn đồng) là nhỏ nhất.
(nghìn đồng) là nhỏ nhất.Vậy gia đình đó mua 0,3 kg thịt bò và 1,1 kg thịt lợn thì chi phí là ít nhất.
Cụ thể là phải chi phí 194 nghìn đồng.
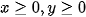 là sản lượng (tấn) cần sản xuất trục sắt và đinh ốc.
là sản lượng (tấn) cần sản xuất trục sắt và đinh ốc.
Ta có:
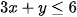 là thời gian hoạt động của máy cắt
là thời gian hoạt động của máy cắt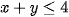 là thời gian hoạt động của máy tiện
là thời gian hoạt động của máy tiệnSố tiền lãi của xưởng sản suất là:
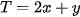 (triệu đồng)
(triệu đồng)Bài toán trở thành: Tìm x, y thỏa mãn
 (*) để
(*) để 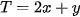 đạt giá trị lớn nhất.
đạt giá trị lớn nhất.Miền nghiệm của hệ bất phương trình (*) là tứ giác OABC
Trong đó
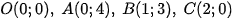
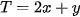 đạt giá trị lớn nhất tại điểm B ứng với
đạt giá trị lớn nhất tại điểm B ứng với 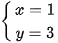
Vậy: Một ngày xưởng nên sản xuất 1 tấn trục sắt và 3 tấn đinh ốc thì tiền lãi cao nhất